Coupling

This is the follow-up to my previous post titled “Orthogonality“.

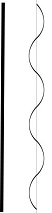
Symbolism: Circle is a geometric symbol of $\mathbb{C}$ (Confinement). Straight line is a geometric symbol of $\mathbb{L}$ (Liberation) .

For the definitions of $\mathbb{C}$ and $\mathbb{L}$ please see the “Orthogonality” article and the references therein.

Initially, the straight line emerges from the center of the circle in a direction perpendicular to the plane of the circle but develops a non-90-degree angle as a result of $\mathbb{C}$ / $\mathbb{L}$ coupling.

In addition to the non-90-degree angle mentioned above, the secondary effect of $\mathbb{C}$ / $\mathbb{L}$ coupling is a distortion (deviation). The simplest form of deviation from the perfect circle is an ellipse.

The simplest form of deviation from the straight line is a wavy line.

Once deviations manifest oscillations start. Oscillation is a type of rotation. The ellipse starts rotating . The rotation of the ellipse can be seen as a shape oscillation. We can imagine the ellipse to be rotating or we can imagine the shape of the ellipse oscillating. These are equivalent descriptions.

As the ellipse rotates (shape oscillates) the non-90-degree angle between the plane of the ellipse and the wavy line will oscillate as well and the wavy line itself will precess around the original perpendicular axis. Many combinations are possible. In fact, there are infinite number of combinations of these oscillation/rotation modes.

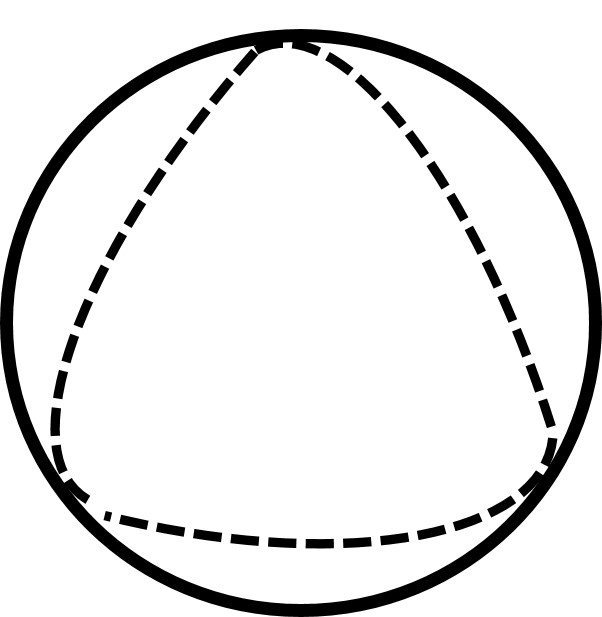
Among the infinite number of oscillation/rotation modes two of them deserve special attention. The simplest form of deviation from a circle is an ellipse but the second most common deformation would be a triangular mode.

The triangular mode exhibits both $\mathbb{C}$ and $\mathbb{L}$ characteristics because in the triangle shape with round corners there are relatively straight line segments which are symbolic expressions of $\mathbb{L}$ . The triangle itself is deformed from a circle which is the symbolic expression of $\mathbb{C}$ .

Another possibility for the deformation of the line is a helix.

The helix mode also exhibits both $\mathbb{L}$ and $\mathbb{C}$ characteristics because the circular motion of the helix is a symbolic expression of $\mathbb{C}$ while the overall progression of the helix symbolizes $\mathbb{L}$ .

Resistance to deformation

By its very nature $\mathbb{L}$ will resist the deformations mentioned above. $\mathbb{L}$ will try to restore the ellipse to the circle, the wavy line to the straight line.

This is similar to the the de-coupling effect of $\mathbb{L}$ mentioned in the “Orthogonality” article. $\mathbb{C}$ keeps breaking orthogonality while $\mathbb{L}$ keeps restoring orthogonality.

$\mathbb{L}$ will try to restore any deformation to the original state. This may not necessarily be a snap back to the original state. The $\mathbb{L}$ reaction may involve a counter formation (inverse of the deviation caused by $\mathbb{C}$ ). In other words, the $\mathbb{L}$ reaction may overshoot causing alternating dominance of the the two factors.

In many posts I mentioned the “primordial fabric”. When $\mathbb{C}$ acts on the primordial fabric and forms a distortion (space-time-matter) $\mathbb{L}$ counters the distortion by forming an inverse distortion. I like the term “dual distortion” also. Stated in different words, we can say that when the perfect symmetry of the primordial fabric is broken, the space-time-matter is formed but at the same time the inverse/dual of the space-time-matter must be formed. This is a huge subject. I kept mentioning this over the years but made little progress in terms of details.

The “inverse/dual deformation” must be proportional to the “deformation”. I suspect there is a fundamental invariance. The { $\mathbb{C} , \mathbb{L}$ } interplay must involve a conservation law. I made few attempts to formulate this fundamental invariance in the past. I hope to tie those older ideas with my recent formulations involving { $\mathbb{C} , \mathbb{L}$ }, cognitive cores, and agency in a future post.

Geometric symbolism is useful

$\mathbb{C}$ and $\mathbb{L}$ are abstract. We see $\mathbb{C}$ and $\mathbb{L}$ expressions in different areas such as physics, chemistry, biology, networks, and mind. The { $\mathbb{C} , \mathbb{L}$ } interplay manifests at many scales. In each area of study and scale we can find different mathematical representations of $\mathbb{C}$ and $\mathbb{L}$ . In principle, we should not restrict ourselves to geometric representation. On the other hand, I find the CLA (circle, line, angle) symbolism very useful.

Measures of coupling

Frequency: We should think of the “oscillation/rotation” of the CLA symbolism abstractly as a measure of coupling strength. The stronger the $\mathbb{C}$ / $\mathbb{L}$ coupling the higher the degree of activity. In the physical stage of manifestation the “degree of activity” translates to “frequency”. When coupled, $\mathbb{C}$ and $\mathbb{L}$ maintain their identities but start turning into each other as a consequence of coupling. This means oscillation/rotation. This also means “activity” or “action” in the abstract sense and “frequency” in the physical sense.

Phase: In physics, phase is the complementary aspect of frequency. Phase is about relative changes of two quantities. Phase is a measure of relative timing between the cycles of two variables. Phase is measured in angle units but it is really about time difference. Both concepts (frequency and phase) require time for a meaningful definition. If I claim that { $\mathbb{C}$ , $\mathbb{L}$ } is abstract and general then I have to have a notion of “abstract time”. Right? I thought about this for a long time. Then I realized that I should work with the concept of “metric” instead of “abstract time”.

Metric: The concept of “metric” refers to a distance measure. We are familiar with the concepts of distance-in-space and distance-in-time. We can think of “phase” as distance in time. The “spacetime metric” concept of the Relativity theory of Einstein is a combination of “distance-in-space” and “distance-in-time”. The concept of “distance” can be abstract. Examples are statistical distance, similarity distance, etc. Since “distance” can be abstract “metric” can also be abstract. The discussion of “metric” in the context of graph theory is very interesting. A mathematical graph is a topological entity. Topology is about connectivity. When we introduce a metric to the graph we obtain a geometrical entity. There are lessons to be learned from graph theory to come up with an abstract metric for the { $\mathbb{C} , \mathbb{L}$ } interplay. More homework for me!

Types of coupling

Alternating: $\mathbb{C}$ and $\mathbb{L}$ might be coupled in such a way that the resultant expression exhibits $\mathbb{C}$ characteristics and $\mathbb{L}$ characteristics in cycles. In this type of coupling $\mathbb{C}$ and $\mathbb{L}$ dominate each other in an alternating fashion.

Steady Mix: The expression (manifestation) may exhibit a steady mix of $\mathbb{C}$ and $\mathbb{L}$ characteristics. In other words the mixing ratio is not changing or alternating but staying relatively constant.

Hyperposed: $\mathbb{C}$ and $\mathbb{L}$ might be coupled in such a way that resembles the superposition described in Quantum Mechanics. This is the inexpressive coupling of the circle and the line perspectives. The expression (manifestation) has not taken form yet. In Quantum Mechanics a measurement (or any interaction) expresses the superposition yielding a particular state of the system. Similarly, a hyperposition will transition to expressive coupling of the circle and the line perspectives as in “steady mix” and “alternating” types.

There must be more types of coupling. In the “Confinement and Liberation” article I listed some of the physical expressions of $\mathbb{C}$ but that’s not an exhaustive list. Clearly, in the course of the evolution of the Cosmos there will be an infinite number of variations in the $\mathbb{C}$ expression. That implies more types or categories of coupling. Think of the increasing agency of human beings. We introduce new organizations, new structures, new formations all the time. This means new types of coupling are manifesting as the Cosmos evolves.

2 or 3 fundamental factors?

In the realm of the mind we have to have at least two factors to explain things. One factor cannot be explanatory. The minimum number of explanatory factors is 2. Hence the { $\mathbb{C}$ , $\mathbb{L}$ } hypothesis.

We may parameterize, however, the “coupling” (symbolized by “angle”) as the third explanatory factor.

{ $\mathbb{L}$ , $\mathbb{C}$ } $\rightarrow$ { $\mathbb{S}$ , $\mathbb{R}$ , $\mathbb{T}$ }

We could identify

$\mathbb{S}$ : Sattvaguna (modified $\mathbb{L}$ )

$\mathbb{R}$ : Rajoguna (symbolized by “angle” representing “coupling”)

$\mathbb{T}$ : Tamoguna (modified $\mathbb{C}$ )

In this model the coupling picture is more complicated. Triangulation requires pair-wise coupling among the 3 factors. This is good and bad. The 3-factor model with pair-wise couplings may provide a richer model but interpreting the details of such a rich model my present interpretational difficulties.

Follow-up articles

Duality Rotation

Coupling

Follow Blog via Email

Pages

Recent Posts

Blog Stats

Coupling

Share this:

Related

Follow Blog via Email

Pages

Recent Posts